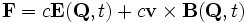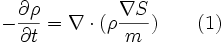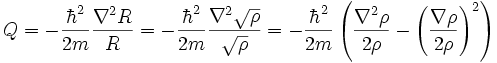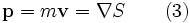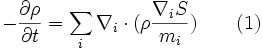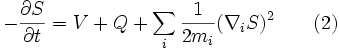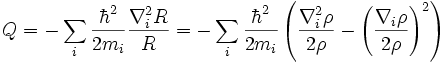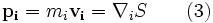Bohm interpretation

From Wikipedia, the free encyclopedia

The neutrality of this article is disputed.
Please see the discussion on the talk page.(December 2007)
Please do not remove this message until the dispute is resolved.

To comply with Wikipedia's quality standards, this article may need to be rewritten.
Please help improve this article. The discussion page may contain suggestions.

The Bohm interpretation of quantum mechanics, sometimes called Bohmian mechanics, the ontological interpretation, or the causal interpretation, is an interpretation postulated by David Bohm in 1952 as an extension of Louis de Broglie's pilot-wave theory of 1927 . Consequently it is sometimes called the de Broglie-Bohm theory. Bohm's interpretation is an example of a hidden variables theory. It is hoped that the hidden variables would provide a local deterministic objective description that would resolve or eliminate many of the paradoxes of quantum mechanics, such as Schrödinger's cat, the measurement problem, the collapse of the wavefunction, and similar concerns. However, Bell's inequality complicates this hope, as it demonstrates that there is no local hidden variable theory that is compatible with quantum mechanics. Thus, one is left with choosing between the lesser of two evils: discarding locality, or discarding realism. The Bohmian interpretation opts for keeping realism and accepting nonlocality.

[hide]

1 Background
- 1.1 Two-slit experiment
- 1.2 Nonlocality
2 Mathematical foundation
3 Benefits
- 3.1 Minimum benefit
4 Beyond Bohm
- 4.1 Seen as isomorphic to many worlds
5 Computational Bohmian Dynamics
6 Criticisms
7 See also
8 References

[edit] Background

The Bohm interpretation can be thought of as taking its cue from what one sees in the laboratory, say, in a two-slit experiment with electrons. We can see localized flashes whenever an electron is detected at some place on the screen. The overall pattern made by many such flashes is governed by a pattern closely matched by simple wave dynamics. Bohm and de Broglie posited that in the world of quantum phenomena, every kind of particle is accompanied by a wave which guides the motion of the particle, hence the term pilot wave. Mathematically, the pilot wave is described by the wavefunction of conventional quantum mechanics, but with an added piloting influence on the motion of the particles.

We can formulate the pilot wave's influence using a wavefunction-derived potential called the quantum potential, which acts upon the particles in a manner analogous to the interaction of particles and fields in classical physics. The pilot wave governs the motion of the particle and evolves according to the Schrödinger equation. Unlike the Everett many-worlds interpretation, the Bohm interpretation does not assume that the universe splits when a measurement occurs, and unlike the Copenhagen interpretation it is both objective and deterministic. It says the state of the universe evolves smoothly through time, with no collapsing of wavefunctions. Thus, Bohm called the hidden variable or pilot wave the quantum potential force.

[edit] Two-slit experiment

In this theory all fundamental entities, such as electrons, are point-like particles that occupy precisely defined regions of space at all times. When one performs a double-slit experiment (see wave-particle duality), one is concerned with noting the positions on a screen at which electrons arrive individually, one at a time. Over time, the positions at which the electrons are detected build up a pattern characteristic of wave interference. The usual Copenhagen interpretation is puzzling in that a single entity, the electron, is said to exhibit characteristics of both particle and wave. The Bohm interpretation accounts for the same phenomena by saying that both a particle and a wave do exist. The particle aspect is present because each electron traverses one slit or another, but never both. The wave aspect is present because the electron's pilot wave traverses both slits.

Thus, the Bohm interpretation resolves the puzzle quite simply and naturally. The electron's motion is guided — both in its choice of slits and its subsequent trajectory towards the screen — by the wave. The characteristic wave-interference pattern seen in the detection of the electrons arises by considering that the guiding wave exhibits interference in the familiar way one learns in the elementary physics of waves.

One might also note that what is measured in such an experiment — the position on the screen at which each electron arrives — is itself none other than the "hidden variable" the Bohm interpretation adds to the description, as we show in the formulation below. It might seem that the term "hidden variables" is an inappropriate name for the positions of particles, the quantity that is apparently most conspicuously manifested in the experiment. However, the particle's position has no influence on the guiding wave and hence is unobservable or "hidden" in some sense (see criticisms).

[edit] Nonlocality

Now we must address the question of nonlocality. Within Bohm's interpretation, it can occur that events happening at one location in space instantaneously influence other events which might be at large distances: thus we say that the theory fails to obey locality, i.e., it is non-local. The response many physicists have to Bohm's theory is often related to how they regard this concept.

The question of nonlocality hinges upon the attitude one takes towards the Einstein-Podolsky-Rosen paradox^[1] and Bell's theorem (see p.14 in^[2]). There are often two camps into which people fall regarding the issue.

According to one camp, it has been shown that quantum mechanics itself is nonlocal and that this cannot be avoided by appealing to any alternative interpretation. The same Bell responsible for Bell's theorem was a member of this group (p. 196 in^[3]): "It is known that with Bohm's example of EPR correlations, involving particles with spin, there is an irreducible nonlocality." If this is indeed the case, then the nonlocality of the Bohm interpretation can hardly be regarded as a strike against it.

Others see the consequences of EPR and Bell's theorem in a different way. They regard the correct conclusion to be related not so much to quantum theory itself, but only to deterministic interpretations of the same (i.e., to hidden-variable theories such as Bohm's interpretation). According to the people who think this way, what has been shown is that all deterministic theories must be nonlocal. For example, Niels Bohr was a member of this group. This group would claim that retaining orthodox quantum mechanics — with its nondeterministic character — permits one to retain locality, or at least to avoid the EPR type of nonlocality, at the expense of having no way to picture particles as objective elements of reality that occupy definite regions of space at all times. Armed with such a viewpoint, these physicists tend to be less receptive to Bohm's interpretation.

In contrast to this, others argue^[4] that non-locality is independent of determinism, counterfactual definiteness and probability factorization, and notes that H.P. Stapp concludes that QM contradicts the locality postulate alone.

[edit] Mathematical foundation

In a rough sense, one might conceptualize Bohm's theory by an analogy with a system of charged particles in motion due to electromagnetic fields. Within electrodynamics, one regards the electric and magnetic fields as functions defined for every position in space and for all times ${\mathbf{E}(\mathbf{q}, t), \mathbf{B}(\mathbf{q},t)}$ . The evolution of these fields is governed by Maxwell's equations.

If we designate the particle position as $\mathbf{Q}$ , then the force on a particle of charge c at some time t is given by

$\mathbf{F} = c \mathbf{E}(\mathbf{Q}, t) + c \mathbf{v} \times \mathbf{B}(\mathbf{Q}, t)$

where we note that the field strength is evaluated at the particle's position $\mathbf{Q}$ in each case.

It is important to note that the fields 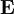$\mathbf{E}$ and $\mathbf{B}$ generally exist throughout space, and hence are defined for all positions $\mathbf{q}$ . The influence they have on the particle depends upon the value they take at the particle's position $\mathbf{Q}$ .

[edit] One-particle formalism

The Schrödinger equation for one particle of mass m is

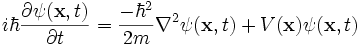$i \hbar \frac{\partial \psi(\mathbf{x},t)}{\partial t} = \frac{-\hbar^2}{2 m} \nabla^2 \psi(\mathbf{x},t)+ V(\mathbf{x}) \psi(\mathbf{x},t)$ ,

where the wavefunction 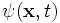$\psi(\mathbf{x},t)$ is a complex function of the spatial coordinate 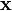$\mathbf{x}$ and time t.

The probability density 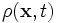$\rho (\mathbf{x},t)$ is a real function defined by

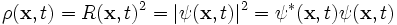$\rho(\mathbf{x},t) = R(\mathbf{x},t)^2 = |\psi(\mathbf{x},t)|^2 = \psi^{*}(\mathbf{x},t) \psi(\mathbf{x},t)$ .

Without loss of generality, we can express the wavefunction 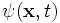$\psi(\mathbf{x}, t)$ in terms of a real probability 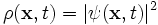$\rho (\mathbf{x},t) = |\psi (\mathbf{x},t)|^2$ and a complex phase that depends on the real variable S, as follows:

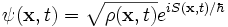$\psi(\mathbf{x},t) = \sqrt{\rho(\mathbf{x},t)} e^{i S(\mathbf{x},t) / \hbar}$ .

The Schrödinger equation can then be split into two coupled equations by taking the real and imaginary terms;

$-\frac{\partial \rho}{\partial t} = \nabla \cdot (\rho \frac{\nabla S}{m}) \qquad (1)$

$-\frac{\partial S}{\partial t} = V + Q + \frac{1}{2m}(\nabla S)^2 \qquad (2)$

where

$Q = -\frac{\hbar^2}{2 m} \frac{\nabla^2 R}{R} = -\frac{\hbar^2}{2 m} \frac{\nabla^2 \sqrt{\rho}}{ \sqrt{\rho}} = -\frac{\hbar^2}{2 m} \left(\frac{\nabla^2 \rho}{2 \rho} -\left(\frac{\nabla \rho}{2 \rho} \right)^2 \right)$

is called the quantum potential. The momentum of Bohm's "hidden variable" particle is defined by

$\mathbf{p} = {m} \mathbf{v} = \nabla S \qquad (3)$

and the particle's energy as 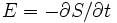$E = - \partial S / \partial t$ ; the particle's position is not yet defined. Equation (1) is interpreted as simply the continuity equation for probability with

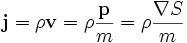$\mathbf{j} = \rho \mathbf{v} = \rho \frac{\mathbf{p}}{m} = \rho \frac{\nabla S}{m}$ ,

and equation (2) is a statement that total energy is the sum of potential energy, quantum potential and the kinetic energy. It is by no means accidental that S has the units and typical variable name of the action.

[edit] Many-particle formalism

The many-particle Schrödinger equation is a straightforward generalisation of the one-particle example:

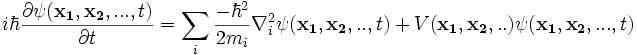$i \hbar \frac{\partial \psi(\mathbf{x_1,x_2,...},t)}{\partial t} = \sum_i \frac{-\hbar^2}{2 m_i} \nabla_i^2 \psi(\mathbf{x_1, x_2,..},t) + V(\mathbf{x_1, x_2,..})\psi(\mathbf{x_1, x_2,...},t)$ ,

where the i-th particle has mass 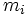$m_i\,$ and position co-ordinate 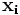$\mathbf{x_i}$ at time t. The wavefunction 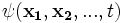$\psi(\mathbf{x_1, x_2,...},t)$ is a complex function of the 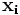$\mathbf{x_i}$ and time t. 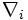$\nabla_i$ is the grad operator with respect to 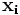$\mathbf{x_i}$ , i.e. of the i-th particle's position co-ordinate. As before the probability density 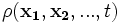$\rho(\mathbf{x_1, x_2,...},t)$ is a real function defined by

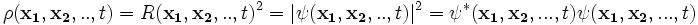$\rho(\mathbf{x_1, x_2,..},t) = R(\mathbf{x_1, x_2,..},t)^2 = |\psi(\mathbf{x_1, x_2,..},t)|^2 = \psi^{*}(\mathbf{x_1,x_2,...},t) \psi(\mathbf{x_1, x_2,...},t)$ .

The complex phase depends on the real variable 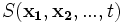$S(\mathbf{x_1, x_2,...},t)$ so that we can define the same relationship as in the 1-particle example:

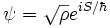$\psi = \sqrt{\rho} e^{i S / \hbar}$ .

Again, the Schrödinger equation can be split into two coupled equations by taking the real and imaginary terms;

$-\frac{\partial \rho}{\partial t} = \sum_i \nabla_i \cdot (\rho \frac{\nabla_i S}{m_i}) \qquad (1)$

$-\frac{\partial S}{\partial t} = V + Q + \sum_i \frac{1}{2m_i}(\nabla_i S)^2 \qquad (2)$

where

$Q = -\sum_i \frac{\hbar^2}{2 m_i} \frac{\nabla_i^2 R}{R} = -\sum_i\frac{\hbar^2}{2 m_i} \left(\frac{\nabla_i^2 \rho}{2 \rho} -\left(\frac{\nabla_i \rho}{2 \rho} \right)^2 \right)$

is the N-particle quantum potential.

The momentum of Bohm's i-th particle's "hidden variable" is defined by

$\mathbf{p_i} = {m_i} \mathbf{v_i} = \nabla_i S \qquad (3)$

and the particles' total energy as 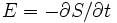$E = - \partial S / \partial t$ ; equation (1) is the continuity equation for probability with

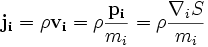$\mathbf{j_i} = \rho \mathbf{v_i} = \rho \frac{\mathbf{p_i}}{m_i} = \rho \frac{\nabla_i S}{m_i}$ ,

and equation (2) is a statement that total energy is the sum of the potential energy, quantum potential and the kinetic energies.

[edit] Commentary on the formalism

Bohm's particle(s) are viewed as having definite positions and velocities at all times, with a probability distribution ρ that may be calculated from the wavefunction ψ. The wavefunction "guides" the particles by means of the quantum potential Q; alternately we can regard the particles' velocities defined by equation (3) -- these two approaches are equivalent.

There is a notable asymmetry with regard to the positions, 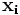$\mathbf{x_i}$ , and velocities, 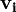$\mathbf{v_i}$ , of the particles. Solving the Schrödinger equation solves for R and S, S immediately yields the particles' velocities, the position can then be found if the initial position is given. However, one can not predict the initial position.

Heisenberg's uncertainty principle states that the accuracy of position and momentum are subjected to the relation of dx dp > h if a measurement is performed. In Bohm's interpretation, there is no uncertainty in position and momentum, therefore a well defined trajectory is possible. In Bohm's picture, well defined trajectories (with precise momentum and position) are there, but we have no control of what trajectory (and thus x and p) will be obtained when we try to find one because we don't know the initial position. If we try to "measure" in order to get more information, we disturb the system and change the trajectory into a new one depending on the measurement set up. The measurement results are subjected to Heisenberg's uncertainty relation. After the measurement, x and p are again well defined, the particle will follow a new trajectory using whatever the new position obtained as the new initial position.

Bohm's picture does not change the fact of Heisenberg's relation. Heisenberg's relation is supported by all experimental results that we know so far. Yet Heisenberg's uncertainty relation implies that we should never talk about trajectories because x and p needed to define a trajectory are not available. Bohm's concept is different in that view point.

In short, there is a difference between "not knowing something" and "something is not there".

The key issue is whether we do measurements.

Put the statement differently, the particles' positions are only known statistically, from R. As in classical mechanics. successive observations of the particles' positions refines or pares away at the initial conditions. Thus, with succeeding observations, the initial conditions become more and more restricted. Yet this formalism is empirically indistinguishable from, and entirely consistent with, the Schrödinger equation, despite the hidden variable Bohm-particles following chaotic paths. It is this underlying chaotic behaviour of the hidden variables that allows the deterministic Bohm theory to generate the apparent indeterminacy associated with each measurement, and hence recover the Heisenberg uncertainty principle. In Bohm's picture, both position and momentum of a particle are well defined. Much of this 1-particle formalism was developed by Louis de Broglie; Bohm extended it from the case of a single particle to that of many particles, and also, by considering the particles in the measuring apparatus, re-interpreted the equations via an early form of quantum decoherence to include observation.

Bohmian mechanics can also be extended to include spin, although the extension to relativistic conditions has not yet been successful.

[edit] Benefits

For supporters, Bohm's interpretation provides a better formulation of quantum mechanics because it is defined more precisely than the Copenhagen interpretation, which is based on theorems that are not expressed in precise mathematical terms but in natural words, like "when measuring." Indeed, the Bohm interpretation subsumes the quantum concepts of measurement, complementarity, decoherence, and entanglement into mathematically precise guidance conditions on position variables. Although it implies the existence of the EPR type of nonlocality, it avoids the need for positing other types of alleged nonlocality, such as wave collapse in Copenhagen interpretation or splitting universes in Many-worlds interpretation.

Many worlds is considered local. See Advantages of many worlds.

[edit] Minimum benefit

The minimum benefit of Bohm's interpretation, independent of the debate about whether it is the preferable formulation, is a disproof of the claim that quantum mechanics implies that particles cannot exist before being measured.

Because it is based on familiar concepts of realism, the Bohm interpretation gives simple, intuitive, non-mystical, and natural answers to what in the standard theory are often perplexing philosophical questions. For example, every particle exists all the time and has a unique position, even when it is not being measured. In the double-slit experiment for electrons, each electron travels through only one slit, but the electron's pilot wave causes the interference pattern. Not only the wave, but the trajectory of each electron can be calculated when one knows the position where the electron hit the screen. This basis in realism strengthens the Bohm interpretation's ties to the concepts of classical physics.

[edit] Beyond Bohm

Bohm's pilot wave theory has been generalized by Antony Valentini of the Perimeter Institute to include signal nonlocality that would allow entanglement to be used as a stand-alone communication channel without a secondary classical "key" signal to "unlock" the message encoded in the entanglement. This violates orthodox quantum theory but it has the virtue that it makes the parallel universes of the cosmic landscape of eternal chaotic inflation observable in principle. This is good news for string theorists although the price to be paid may be too high for many. Valentini cites earlier work that shows that orthodox quantum theory corresponds to "sub-quantal thermal equilibrium" for the hidden variables. The larger theory is a non-equilibrium theory. Still another way to look at this is to recognize that orthodox quantum theory in Bohm's ontology is a test particle approximation like in general relativity. That is, the hidden variable "particles" and "field configurations" receive their marching orders from the pilot quantum information wave but do not directly react back on the pilot wave. Bohm and Hiley briefly discuss this in Ch 14 of the "Undivided Universe." This direct feedback of particle on its guiding pilot wave introduces an instability, a feedback loop that pushes the hidden variables out of thermal equilibrium "sub-quantal heat death" (Valentini). The resulting theory becomes nonlinear and non-unitary. The Born probability interpretation can no longer be sustained in this emergence of new order in complex systems that P.W. Anderson has called "More is different."

[edit] Seen as isomorphic to many worlds

Explicitly non-local. Bohm accepts that all the branches of the universal wavefunction exist. Like Everett, Bohm held that the wavefunction is real complex-valued field which never collapses. In addition Bohm postulated that there were particles that move under the influence of a non-local "quantum- potential" derived from the wavefunction (in addition to the classical potentials which are already incorporated into the structure of the wavefunction). The action of the quantum- potential is such that the particles are affected by only one of the branches of the wavefunction. (Bohm derives what is essentially a decoherence argument to show this, see section 7,#I [B]).

The implicit, unstated assumption made by Bohm is that only the single branch of wavefunction associated with particles can contain self-aware observers, whereas Everett makes no such assumption. Most of Bohm's adherents do not seem to understand (or even be aware of) Everett's criticism, section VI [1], that the hidden- variable particles are not observable since the wavefunction alone is sufficient to account for all observations and hence a model of reality. The hidden variable particles can be discarded, along with the guiding quantum-potential, yielding a theory isomorphic to many-worlds, without affecting any experimental results.

—Michael Clive Price[1]

[edit] Computational Bohmian Dynamics

Most of the discussion in this page focuses upon interpretation and ontological consequences of Bohm's formalism. However, it is mathematically valid and provides a potentially novel way to perform quantum mechanical calculations. Work by Robert Wyatt in the early 2000's attempted to use the Bohm "particles" as an adaptive mesh that follows the actual trajectory of a quantum state in time and space. In the "quantum trajectory" method, one samples the quantum wave function with a mesh of quadrature points. One then evolves the quadrature points in time according to the Bohm equations of motion written above. At each time-step, one then re-synthesizes the wave function from the points, recomputes the quantum forces, and continues the calculation. Quick-time movies of this for H+H₂ reactive scattering can be found on the Wyatt group web-site at UT Austin.

This approach has been adapted, extended, and used by a number of researchers in the Chemical Physics community as a way to compute semi-classical and quasi-classical molecular dynamics. A recent issue of the Journal of Physical Chemistry A was dedicated to Prof. Wyatt and his work on "Computational Bohmian Dynamics". Eric Bittner's group at the University of Houston has advanced a statistical variant of this approach that uses Baysian sampling technique to sample the quantum density and compute the quantum potential on a structureless mesh of points. This technique was recently used to estimate quantum effects in the heat-capacity of small clusters Ne_n for n~100.

There remain difficulties using the Bohmian approach, mostly associated with the formation of singularities in the quantum potential due to nodes in the quantum wave function. In general, nodes forming due to interference effects lead to the case where 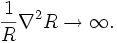$\frac{1}{R}\nabla^2R\rightarrow\infty.$ This results in an infinite force on the sample particles forcing them to move away from the node and often times crossing the path of other sample points (which violates single-valuedness). Various schemes have been developed to overcome this; however, no general solution has yet emerged.

There has also been recent work in developing Complex Bohmian trajectories which satisfy isochronal relations.

[edit] Criticisms

The main points of critics, together with the responses of Bohm-interpretation advocates, are summarized in the following points:

Bohm's interpretation does not reproduce quantum field theory, which is the modern theory of quantum mechanics, which has been verified experimentally remarkably well. Since locality is essential to quantum field theory, it is unclear that it is possible to reproduce it via Bohm's interpretation.

Response: A Bohmian interpretation of quantum field theory also exists (see, e.g.,[2], [3], and references therein) and reproduces all measurable predictions of quantum field theory. Although this Bohmian theory is not local at the fundamental level, all local properties of quantum field theory are reproduced.

The main weakness of Bohm's theory is that it looks contrived — and gives the same measurable predictions which are in all details identical to conventional quantum mechanics, so it is not really a scientific theory.

Response: Bohm deliberately designed his theory to give the same predictions as the conventional approach. His original aim was not to make a serious counterproposal but simply to demonstrate that hidden-variables theories are indeed possible, contrary to the earlier belief (due to von Neumann) that they are not possible. To accomplish this aim it was necessary that the predictions of the two theories be the same. However, Bohm's hope was that this demonstration could lead to new insights and experiments. Bohm's theory can be extended in ways that cannot even be contemplated in the conventional theory, and these extensions may lead to new measurable predictions.

Furthermore, in clarifying theoretical issues such as nonlocality the theory already has been highly successful. The theory inspired John Stewart Bell to prove his now-famous theorem,^{[citation needed]} which in turn led to the Bell test experiments. This would be a rather amazing accomplishment for a theory that is "not really scientific."

The wavefunction must "disappear" or "collapse" after a measurement, and this process seems highly unnatural in the Bohmian models.

Response: Collapse is a main feature of von Neumann's theory of quantum measurement. In the Bohm interpretation, a wave does not collapse. Instead, a measurement produces what Bohm called "empty channels" consisting of portions of the wave that no longer affect the particle. This explains why physical systems behave as if parts of the wavefunction had disappeared, despite the fact that there is no true disappearance or collapse. (The process whereby a quantum system interacts with its environment to give the appearance of wavefunction collapse is called decoherence.)

The theory artificially picks privileged observables: while orthodox quantum mechanics admits many observables on the Hilbert space that are treated almost equivalently (much like the bases composed of their eigenvectors), Bohm's interpretation requires one to pick a set of "privileged" observables that are treated classically — namely the position. There is no experimental reason to think that some observables are fundamentally different from others. For instance measuring the frequency of a radio signal requires absorption of photons across the entire receiving antenna (i.e. the photons are measured as spatially delocalized entities). Another more direct example, drawn from the example of our senses, is the perception (measurement) of colour which is the measurement of a photon's frequency (again), which requires that the photon be delocalised, by the Heisenberg uncertainty principle. In this example the delocalisation is confined to the diameter of a pigment molecule in the retina, instead of an antenna, but the effect is a real one.

Response: Every physical theory can be rewritten based on different fundamental variables without being different empirically. The Hamilton-Jacobi equation formulation of the classical mechanics is an example. Positions may be considered as a natural choice for the selection because positions are most directly measurable. For example, one does not actually measure the "spin" of a particle in the Stern–Gerlach experiment, but instead measures the position of the light flashes on a detector. Often the observed quantities are positions, e.g. of a measuring needle or of the particles making up a computer display. And so there is justification for privileging position.

The Bohmian models are truly nonlocal: this nonlocality violates Lorentz invariance; contradictions with special relativity are therefore expected; they make it highly nontrivial to reconcile the Bohmian models with up-to-date models of particle physics, such as quantum field theory or string theory, and with some very accurate experimental tests of special relativity, without some additional explanation. On the other hand, other interpretations of quantum mechanics, such as consistent histories or the many-worlds interpretation, allow us to explain the experimental tests of quantum entanglement without any nonlocality whatsoever.

Response: Nonlocality and Lorentz invariance are not in contradiction. An example of a nonlocal Lorenz-invariant theory is the Feynman-Wheeler theory of electromagnetism.

Furthermore, it is questionable whether other interpretations of quantum theory are in fact local or are simply less explicit about nonlocality. See for example the EPR type of nonlocality. And recent tests of Bell's Theorem add weight to the belief that all quantum theories must abandon either the principle of locality or counterfactual definiteness (the ability to speak meaningfully about the definiteness of the results of measurements, even if they were not performed).

That said, it is true that finding a Lorentz-invariant expression of the Bohm interpretation (or any similar nonlocal hidden-variable theory) has proved difficult, and it remains an open question for physicists today whether such a theory is possible and how it would be achieved.

The Bohmian interpretation has subtle problems with incorporating spin and other concepts of quantum physics: the eigenvalues of the spin are discrete, and therefore contradict rotational invariance unless the probabilistic interpretation is accepted.

Response: This criticism is based on the false assumption that the particle position variables in Bohm's equations must carry spin. There are natural variants of the Bohm interpretation in which such problems do not appear. In these, spin is a property of the wave only; the particle variables have no spin in the mathematical formulation.

The Bohmian interpretation also seems incompatible with modern insights about decoherence that allow one to calculate the "boundary" between the "quantum microworld" and the "classical macroworld"; according to decoherence, the observables that exhibit classical behavior are determined dynamically, not by an assumption.

Response: When the Bohm interpretation is treated together with the von Neumann theory of quantum measurement, no incompatibility with the insights about decoherence remains. On the contrary, the Bohm interpretation may be viewed as a completion of the decoherence theory. It provides an answer to the question that decoherence by itself cannot answer: What causes the system to pick up a single definite value of the measured observable? And the fact that the theory does not postulate the existence of any boundary between two "worlds" can be viewed as one of its major advantages.

Another possible route to new predictions is opened up by current developments in quantum chaos. In this theory, there exist quantum wave functions that are fractal and thus differentiable nowhere. While such wave functions can be solutions of the Schrödinger equation, taken in its entirety, they would not be solutions of Bohm's coupled equations for the polar decompsition of ψ into ρ and S, given above. The breakdown occurs when expressions involving ρ or S become infinite (due to the non-differentiability), even though the average energy of the system stays finite, and the time-evolution operator stays unitary. As of 2005, it does not appear that experimental tests of this nature have been performed.

The Bohm interpretation involves reverse-engineering of quantum potentials and trajectories from standard QM. Diagrams in Bohm's book are constructed by forming contours on standard QM interference patterns and are not calculated from his "mathematical" formulation. Recent experiments with photons arXiv:quant-ph/0206196 v1 28 Jun 2002 favor standard QM over Bohm's trajectories.

Response: The Bohm interpretation takes the Schrödinger equation even more seriously than does the conventional interpretation. In the Bohm interpretation, the quantum potential is a quantity derived from the Schrödinger equation, not a fundamental quantity. Thus, the interference patterns in the Bohm interpretation are identical to those in the conventional interpretation. As shown in [4] and [5], the experiments cited above only disprove a misinterpretation of the Bohm interpretation, not the Bohm interpretation itself.

The Bohm particles are not observable entities and are therefore unnecessary, as for example the luminiferous ether was found to be unnecessary in special relativity. In the Bohm interpretation, we can remove the particles from the theory and still account for all our observations, since Bohm regards the universal wavefunction as a complex-valued but real field that never collapses. This was first noted by Hugh Everett who showed that the wavefunction is sufficient explanation for all our observations; see section 6.c of The Theory of the Universal Wavefunction, which claims that the hidden-variable particles can't be observed at all, directly or indirectly. This unobservability stems from an asymmetry in the causal structure of the theory: the wavefunction influences the position and velocity of the hidden variables, but the hidden variables do not influence the time development of the wavefunction.

Response: Bohm accepted that the particles in his interpretation cannot be observed directly, but nevertheless he thought the concept of particles having definite positions even when unobserved contributes to the theory, so, in Bohm's view, the comparison to the luminiferous ether is invalid. Bohm maintained that the wavefunction alone is not a sufficient explanation for all our observations; in Bohm's view particles are needed simply to account for why we observe one particular outcome of an experiment rather than a superposition of outcomes, as in the paradox of Schrödinger's cat. Without particles, some additional process such as collapse, decoherence, or splitting universes is necessary to connect quantum theory to experience.

[edit] See also

At Wikiversity, you can learn about:

Making sense of quantum mechanics

[edit] References

^ Einstein, Podolsky, Rosen Can Quantum Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 47, 777 (1935).
^ Bell, John S, Speakable and Unspeakable in Quantum Mechanics, Cambridge University Press 1987.
^ Bell, John S, Speakable and Unspeakable in Quantum Mechanics, Cambridge University Press 1987.
^ Ballentine, L.E., Quantum Mechanics, A Modern Development, P.608, "...Therefore determininisum cannot be the cause of the contradiction...

Albert, David Z. (May 1994). "Bohm's Alternative to Quantum Mechanics". Scientific American.
Barbosa, G. D.; N. Pinto-Neto (2004). "A Bohmian Interpretation for Noncommutative Scalar Field Theory and Quantum Mechanics". Physical Review D 69: 065014. arXiv:hep-th/0304105.
Bohm, David (1952). "A Suggested Interpretation of the Quantum Theory in Terms of "Hidden Variables" I". Physical Review 85: 166-179.
Bohm, David (1952). "A Suggested Interpretation of the Quantum Theory in Terms of "Hidden Variables", II". Physical Review 85: 180-193.
Bohm, David (1990). "A new theory of the relationship of mind and matter". Philosophical Psychology 3 (2): 271-286.
Bohm, David; B.J. Hiley (1993). The Undivided Universe: An ontological interpretation of quantum theory. London: Routledge. ISBN 0-415-12185-X.
Durr, Detlef; Sheldon Goldstein, Roderich Tumulka and Nino Zangh (December 2004). "Bohmian Mechanics".
Goldstein, Sheldon (2001). "Bohmian Mechanics". Stanford Encyclopedia of Philosophy.
Hall, Michael J.W. (2004). "Incompleteness of trajectory-based interpretations of quantum mechanics". arXiv:quant-ph/0406054. (Demonstrates incompleteness of the Bohm interpretation in the face of fractal, differentialble-nowhere wave functions.)
Holland, Peter R. (1993). The Quantum Theory of Motion : An Account of the de Broglie-Bohm Causal Interpretation of Quantum Mechanics. Cambridge: Cambridge University Press. ISBN 0-521-48543-6.
Nikolic, H. (2004). "Relativistic quantum mechanics and the Bohmian interpretation". arXiv:quant-ph/0406173.
Passon, Oliver (2004). "Why isn't every physicist a Bohmian?". arXiv:quant-ph/0412119.
Sanz, A. S.; F. Borondo (2003). "A Bohmian view on quantum decoherence". arXiv:quant-ph/0310096.
Sanz, A.S. (2005). "A Bohmian approach to quantum fractals". J. Phys. A: Math. Gen. 38. (Describes a Bohmian resolution to the dilemma posed by non-differentiable wave functions.)
Streater, Ray F. (2003). Bohmian mechanics is a "lost cause". Retrieved on 2006-06-25.
Valentini, Antony; Hans Westman (2004). "Dynamical Origin of Quantum Probabilities". arXiv:quant-ph/0403034.
Bohmian mechanics on arxiv.org

Retrieved from "http://en.wikipedia.org/wiki/Bohm_interpretation"

Bohm interpretation

From Wikipedia, the free encyclopedia

Contents

[edit] Background

[edit] Two-slit experiment

[edit] Nonlocality

[edit] Mathematical foundation

[edit] One-particle formalism

[edit] Many-particle formalism

[edit] Commentary on the formalism

[edit] Benefits

[edit] Minimum benefit

[edit] Beyond Bohm

[edit] Seen as isomorphic to many worlds

[edit] Computational Bohmian Dynamics

[edit] Criticisms

[edit] See also

[edit] References

Views

Personal tools

Navigation

Interaction

Search

Toolbox

Languages